Pierre-Carl Michaud, 20 avril 2021

Structure de population

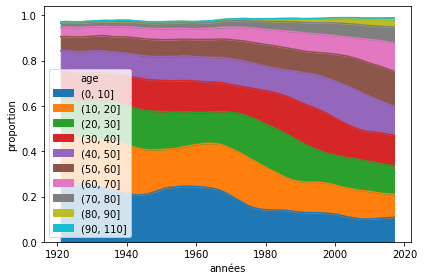
Quand on parle de vieillissement, on a tendance à regarder l’évolution de la structure d’âge de la population au Québec. Et bien sûr, on en conclut que le Québec vieillit assez rapidement. Ici j’utilise les données de la Banque de données sur la longévité canadienne pour le Québec. Je laisse les traces de mes codes Python pour ceux qui voudraient refaire ces calculs.

Après le baby boom du milieu du siècle dernier, on voit que la part des moins de 40 ans a chuté considérablement. Le boom et l’écho de David Foot et sa transmission dans la structure d’âge se voit à l’oeil nu.

import numpy as np 
import pandas as pd
from matplotlib import pyplot as plt

pop = pd.read_csv('Population.csv',sep=';')
pop.set_index(['Year','Age'],inplace=True)
pop = pop['Total'].unstack()
pop = pop.transpose()
pop = pop[pop.index>=0]

shares = pop.copy()
for s in shares.columns:
    shares.loc[:,s] = pop.loc[:,s]/pop[s].sum()

shares['gr_age'] = pd.cut(shares.index,bins=[0,10,20,30,40,50,60,70,80,90,110])
shares = shares.groupby('gr_age').sum()
shares.index.name = 'age'

plt.figure()
shares.transpose().plot.area()
plt.xlabel('années')
plt.ylabel('proportion')
plt.tight_layout()
plt.savefig('aging.png',dpi=1200)
plt.show()

Espérance de vie

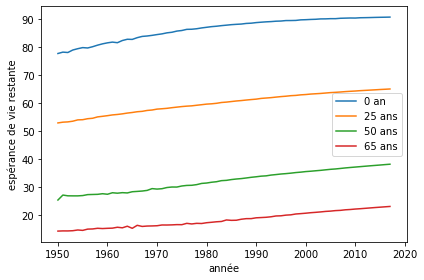
Mais une tendance qu’on ne voit pas facilement dans la structure d’âge est l’amélioration de l’espérance de vie, en particulier par génération. J’utilise ici les tables de mortalité de l’ISQ par génération. On peut les manipuler pour faire une table année par âge. On peut voir l’augmentation quasi constante de l’espérance de vie dans le siècle dernier. Quelqu’un né en 1950 avant une espérance de vie d’un peu moins de 80 ans. Quelqu’un né en 2020 a une espérance de vie de plus de 90 ans. Notons que ces chiffres diffèrent des calculs d’espérance de vie du moment puisqu’on regarde prospectivement ici l’espérance de vie alors qu’une table du moment utilise les taux de mortalité de l’année courante pour calculer l’espérance de vie. Ainsi les espérances de vie par générations sont généralement plus élevées dans un contexte d’amélioration constante des taux de mortalité.

exc = pd.read_excel('esperance_scenario-1861-2026.xlsx')
exc.set_index('age',inplace=True)
exc = exc.stack()
exc.index.names = ['age','byr']
exc = exc.reset_index()
exc['year'] = exc['age'] + exc['byr']
exc.columns = ['age','byr','ex','year']
exc = exc[['age','year','ex']]
exc.set_index(['age','year'],inplace=True)
exc = exc.unstack()
exc.columns = [x[1] for x in exc.columns]
exc = exc[[x for x in range(1950,2018)]]
for x in range(2016,1949,-1):
    exc.loc[exc[x].isna(),x] = exc.loc[exc[x].isna(),x+1].copy()
exc = exc[exc.index>=0]

plt.figure()
plt.plot(exc.columns,exc.loc[0,:],label='0 an')
plt.plot(exc.columns,exc.loc[25,:],label='25 ans')
plt.plot(exc.columns,exc.loc[50,:],label='50 ans')
plt.plot(exc.columns,exc.loc[65,:],label='65 ans')
plt.xlabel('année')
plt.ylabel('espérance de vie restante')
plt.legend()
plt.tight_layout()
plt.show()

Age réel

C’est donc dire que quelqu’un de plus âgé aujourd’hui a une espérance de vie comparable à celle d’une personne plus jeune d’autrefois. On peut trouver dans une année donnée l’âge de la personne ayant la même espérance de vie pour une année de référence. Ceci nous donne un âge réel qui prend en compte que la mort est plus distante aujourd’hui à un âge donné qu’elle l’était autrefois. Voici comment faire.

On débute par faire une clé d’interpolation dans une année de référence qui donnera l’âge de la personne ayant une espérance de vie donnée. On choisi 1950 comme année de référence. Voici cette clé, ou fonction, en python.

from scipy.interpolate import interp1d
f = interp1d(exc[1950].values,exc[1950].index.values,fill_value='extrapolate')

On applique maintenant à chaque année et âge cette clé pour calculer l’âge réel. Puisque les personnes plus jeunes pourraient avoir un âge réel négatif, on code à zéro.

ages = exc.copy()
for x in exc.columns:
    ages[x] = f(exc[x])
ages[ages<0] = 0

Voici un aperçu sous forme de tableau de ce que cela donne. On peut voir qu’une personne de 35 ans en 2016 a un âge réel de 23.92 années en termes d’espérance de vie de 1950. Une personne de 65 ans en 2016 a un âge réel de 53.93 ans. C’est ce qui fait dire à Boyer et Boyer 2013 que la population rajeunie alors que l’on croit qu’elle vieillit.

ages.loc[[35,45,55,65,75],[1950,1956,1976,1996,2016]]

	1950	1956	1976	1996	2016
âge
35	35.0	33.915888	29.550847	26.366667	23.920792
45	45.0	44.090164	39.954839	35.934783	33.289720
55	55.0	53.701613	50.089552	46.642857	43.473684
65	65.0	63.924242	61.168421	57.565217	53.927419
75	75.0	74.352941	70.410256	68.837838	64.924242

Combiner ces effets pour obtenir l’âge réel moyen

Alors que pour un âge donné, l’âge réel diminue, il est aussi vrai que la population est plus âgée qu’elle ne l’était par le phénomène de vieillissement collectif. L’évolution de la structure d’âge de la population tend à augmenter l’âge réel alors que l’augmentation de l’espérance de vie le fait diminuer. On peut combiner ces effets pour voir l’effet net.

table = pd.DataFrame(index=exc.columns,columns=['age_real','age_real_f','age'])
age_real_f = []
for x in exc.columns:
    age_real_f.append((pop[1950]*ages[x]).sum()/pop[1950].sum())
table['age_real_f'] = age_real_f
age_real = []
for x in exc.columns:
    age_real.append((pop[x]*ages[x]).sum()/pop[x].sum())
table['age_real'] = age_real
for x in exc.columns:
    table.loc[x,'age'] = (pop.index * pop[x]).sum()/pop[x].sum()

plt.figure()
plt.plot(table.index,table.age,label='âge moyen')
plt.plot(table.index,table.age_real_f,label='âge réel (pop const. 1950)')
plt.plot(table.index,table.age_real,label='âge réel')
plt.legend()
plt.ylabel('âge')
plt.xlabel('année')
plt.tight_layout()
plt.savefig('younger.png',dpi=1200)
plt.show()

Sans considération pour l’âge réel, l’âge moyen de la population au Québec a presque doublé sur la période. À structure de population constante, l’âge moyen réel a quant à lui diminué parce que l’espérance de vie elle augmente à tous les âges. Quand on combine les deux tendances, on peut observer un léger vieillissement, mais beaucoup plus faible!

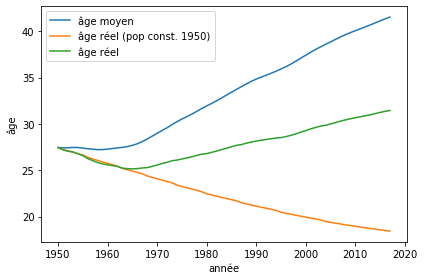
Ceci illustre qu’il y a beaucoup de potentiel au niveau du marché du travail afin de bénéficier de cette augmentation de l’âge réel. Mais encore faut-il encourager la population à demeurer active plus longtemps afin d’amoindrir les effets du vieillissement démographique sur l’économie et les finances publiques.