Introduction¶

Théorie et données¶

Le site missingprofits.world calcule ce que perd chaque pays aux paradis fiscaux. Mais comment rapatrier ces profits? Quel effet aurait une taxe sur la richesse pour réduire les inégalités? On a besoin de la théorie pour comprendre l’effet potentiel des incitatifs. Ensuite, les données pour estimer ces effets. Les économistes Emmanuel Saez et Gabriel Zucman s’intéressent à cette question avec théorie et données.

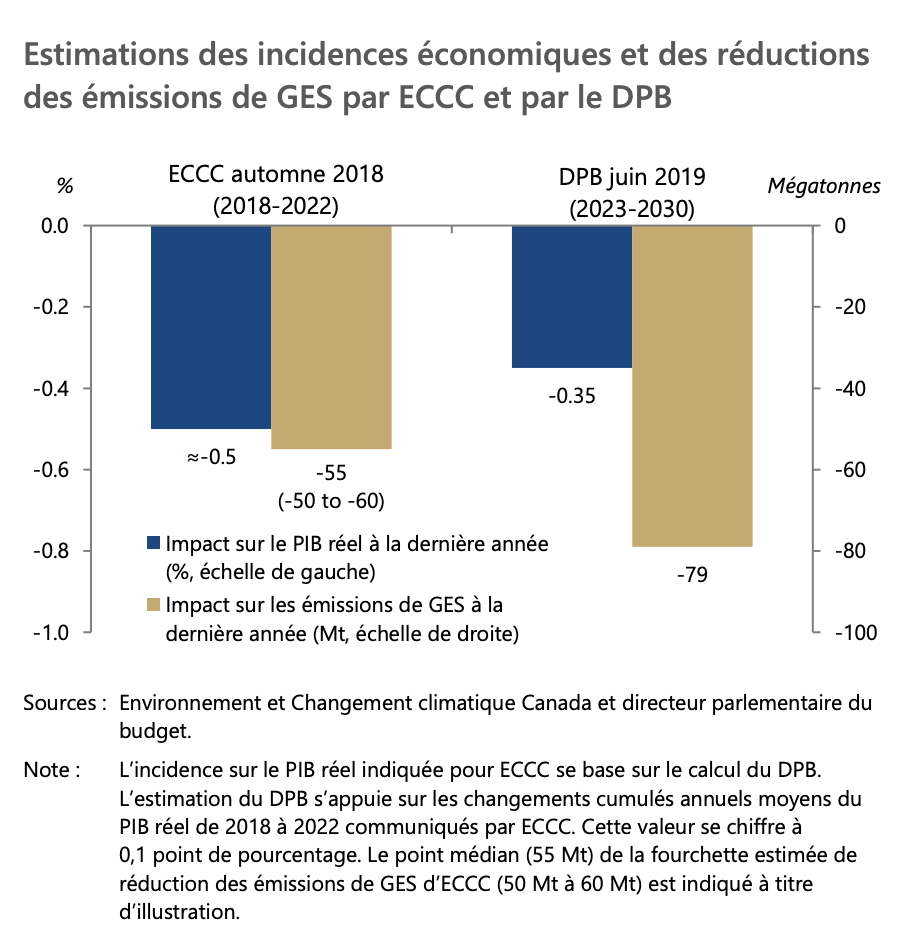
Une taxe sur le carbone pourrait être un bon moyen de lutter contre le réchauffement climatique. Mais quels sont les effets d’une telle taxe sur l’économie? En 2019, le Directeur parlementaire du Budget du Canada dans un rapport utilise un modèle d’équilibre général pour calculer ces effets. Le modèle utilise données et théorie.

Comment structurer le marché de la publicité sur internet? Quel est le prix de l’information? Comment rémunérer le classement dans les moteurs de recherche? Hal Varian est l’économiste en chef chez Google. Il est l’auteur d’un livre de théorie très populaire en microéconomie, mais aussi quelqu’un qui conjugue au quotidien données et théorie pour aider les entreprises de la nouvelle économie. Voir cette entrevue avec lui.

Les données sont partout. La théorie aide à en faire du sens:

Comprendre les comportements (e.g. tester des théories)
Quantifier des effets pour porter des jugements sur des politiques
Tarification et optimisation en entreprise

Voir aussi

Cet article de Judea Pearl, pourtant un des pionniers de l’intelligence articifielle, met en garde contre une utilisation des données sans cadre théorique.

Rappel mathématique¶

Les mathématiques sont essentielles, en particulier le calcul différentiel, afin d’analyser le comportement, mesurer l’effet de changements dans l’environnement (prix, taxes). Voici un (rappel) des concepts qui sont importants pour le cours.

L’analyse marginale et les approximations¶

Comment décrire une fonction \(f(x)\)?

Fonctions généralement compliquées, fonctions linéaires simples… En python, voici comment écrire une fonction.

def f(x):
  return x**2
def g(x):
  return 1/x

Localement, on peut faire une approximation de toute fonction lisse pour \(x\) près de \(x_0\):

\[f(x) \simeq f(x_0) + \alpha (x-x_0)\]

Voici une approximation, pour un \(\alpha\) donné:

def fa(x,x0,alpha):
  return f(x0) + alpha * (x - x0)

Pour trouver le meilleur \(\alpha\), on a que pour \(x\) près de \(x_0\)

\[\begin{split}&f(x) \simeq f(x_0) + \alpha (x-x_0) \\ \\ \iff & f(x) -f(x_0) \simeq \alpha (x-x_0)\\\\ \iff & \alpha \simeq \frac{f(x) -f(x_0)}{x-x_0}\end{split}\]

En python,

x = 2
x0 = 1
alpha = (f(x) - f(x0))/(x-x0)

Important

Une approximation est juste si la différence \(\epsilon = x - x_0\) est faible.

Donc, on peut définir

\[f'(x_0) = \lim_{\epsilon \to 0} \frac{f(x_0+\epsilon) - f(x_0)}{\epsilon}\]

On peut toujours calculer une dérivée numériquement en utilisant un \(\epsilon\) petit:

def fp(x0):
   eps = 1e-6
   return (f(x0+eps) - f(x0))/eps

et alors, l’approximation devient

\[\begin{split}f(x) \simeq f(x_0) + f'(x_0) (x-x_0) \\ f(x) - f(x_0) \simeq f'(x_0) (x-x_0) \\ \Delta f \simeq f'(x_0) \Delta x\end{split}\]

En python, on peut écrire

def fa(x,x0):
  return f(x0) + fp(x0)*(x-x0)

Si on veut prédire le changement dans la valeur d’une fonction, la dérivée est donc très utile! Pour plusieurs types de fonctions, on peut trouver l’expression de la dérivée sans faire un calcul numérique…

La dérivée¶

Voici des recettes:

Avec des constantes

\(f(x) = b + ax\): \(f'(x) = a\)
\(f(x) = \log x\): \(f'(x) = \frac{1}{x}\)
\(f(x) = e^{ax}\): \(f'(x) = ae^{ax}\)
\(f(x) = x^a\): \(f'(x) = a x^{a-1}\)

Avec des fonctions

Règle du produit: \(f(x) = a(x)b(x)\), \(f'(x) = a'(x)b(x) + a(x)b'(x)\)
Règle du quotient: \(f(x) = \frac{a(x)}{b(x)}\), \(f'(x) = \frac{a'(x)b(x) - a(x)b'(x)}{b(x)^2}\)
Règle de chaine: \(f(x) = a(b(x))\), \(f'(x) = a'(b(x))b'(x)\)
Règle d’addition (et soustraction): \(f(x) = a(x) + b(x)\), \(f'(x) = a'(x) + b'(x)\).

À faire

Exercice A: Trouvez les dérivées de \(f(x)=\sqrt{x},\frac{x}{1+x},\frac{1}{2}x^2 + 2x-10,(1+\frac{x}{2})^2\).

À faire

Exercice B: Faire une approximation de premier ordre pour \(f(x)=\sqrt{x}\).

Approximations d’ordres supérieurs

Si la fonction a des dérivées supérieures non nulles, ou bien \(x\) est loin de \(x_0\), l’approximation de premier ordre que nous avons vu produira une approximation assez mauvaise… Par ailleurs, on veut peut-être aussi caractériser des fonctions par autre chose que seulement leur pente. (est-ce une courbe, etc?).

On peut pousser plus loin le concept d’approximation,

Polynome d’ordre 2 devrait être meilleur…
Alors, on approxime par deuxième ordre
Polynome d’ordre \(k\): on peut certainement généraliser.

Ce type d’approximation est appelée approximation de Taylor. On utilise alors les dérivées d’ordres supérieurs d’une fonction:

\[f(x) = f(x_0) + f'(x_0)(x-x_0) +\frac{1}{2}f''(x_0)(x-x_0)^2 + \ldots\]

On dénote \(f'(x), f''(x)\) ou \(\frac{d f}{d x},\frac{d}{d x}(\frac{d f}{d x}) = \frac{d^2 f}{d x^2}\).

Concavité et Convexité des fonctions

Une fonction est concave si pour tout point \((x_1,x_2)\) et tout \(0<\lambda<1\):

\[f(\lambda x_1 + (1-\lambda) x_2) \geq \lambda f(x_1) + (1-\lambda)f(x_2)\]

et convexe si faux. On dit strictement concave (ou convexe) si les inégalités sont strictes (n’incluent pas zéro).

Note

En d’autres termes, si pour toutes les pairs de points, la ligne qui les rejoints est en dessous de la fonction, la fonction est concave. Si c’est l’opposé, elle est convexe.

Approximation et maximum (minimum)

Considérons l’approximation de premier ordre

\[f(x_0+\Delta x) \simeq f(x_0)+ f'(x_0)\Delta x.\]

Observons que:

Si \(f'(x_0)>0\) un petit changement \(\Delta x>0\) augmente \(f\)
Si \(f'(x_0) <0\) un petit changement \(\Delta x <0\) augmente \(f\)
Si \(x_0\) est la solution de \(\max_x f(x)\), il faut que \(f'(x_0) =0\)! C’est la condition de premier ordre (CPO) nécessaire.

Considérons l’approximation de deuxième ordre pour voir si elle est suffisante:

\[f(x_0+\Delta x) \simeq f(x_0) + f'(x_0)\Delta x +\frac{1}{2}f''(x_0)\Delta x ^2\]

Pour un maximum (local), il faut que \(f'(x_0)=0\) (condition de premier ordre, CPO) et \(f''(x_0)<0\) (condition de deuxième ordre, CDO). Observons que:

Si \(f'(x_0) = 0\), mais \(f''(x_0)>0\), alors \(f(x_0+\Delta x) > f(x_0)\).
f’(x) doit être positif quand \(\Delta x <0\) et négatif quand \(\Delta x>0\).

Avertissement

La condition de premier ordre est nécessaire mais n’est pas suffisante. Une fonction qui a un point d’inflection, aura une CPO respectée sur le point de scelle sans pour autant que ce point soit un maximum. La CDO prévient de cas de figure.

À faire

Exercice C: Trouvez l’optimum de la fonction \(f(x) = x(10-x)\).

Dérivée partielle¶

Supposons la fonction \(f(x,y)\). La dérivée partielle se fait en gardant fixes (ou exogènes) les autres variables: \(f'_x(x,y) = \frac{\partial f(x,y)}{\partial x}\).

Note

Une dérivée partielle ne représente donc pas de difficulté additionelle. On peut revoir le cas de figure ici-haut, \(f(x) = ax\) comme étant \(g(x,a) = a x\) et donc \(g'_x(x,a) = f'(x) = a\).

La différentielle totale¶

Les combinaisons de \(x,y\) telles que \(f(x,y) = \overline{f}\)) peuvent être trouvées en inversant la fonction, \(y=g(x,\overline{f})\). Mais on peut décrire ces combinaisons en utilisant la différentielle totale (une approximation linéaire):

On peut décrire la forme d’une fonction à un point donné par:

\[\begin{aligned} df(x,y) = f'_x(x,y)dx + f'_y(x,y)dy\end{aligned}\]

Si on pose \(df(x,y)=0\), on peut réarranger pour obtenir

\[\frac{dy}{dx}\Bigr|_{df=0} = -\frac{f'_x(x,y)}{f'_y(x,y)}\]

On qualifie la dérivée par le \(df=0\) pour indiquer que c’est une dérivée obtenue en contraignant la valeur de la fonction à être constante.

À faire

Exercice D: Trouvez \(\frac{dy}{dx}\Bigr|_{df=0}\) par différentielle totale pour \(f(x,y)=\log(xy)\). Faire sur papier et par SymPy.

Homogénéité d’une fonction¶

La dérivée partielle informe sur le comportement de la fonction quand un des arguments varie alors que les autres demeurent constants. Mais on pourrait aussi s’intéresser au comportement d’une fonction quand tous les arguments augmentent (ou diminuent) d’une même proportion. On utilise le concept d’homogénéité. Il y a deux façons de s’y prendre:

Approche directe: Une fonction est homogène de degré \(r\) si pour tout \(\lambda>0\),

\[f(\lambda x_1, \lambda x_2, ... \lambda x_n) = \lambda^r f(x_1,x_2,...,x_n)\]

Théorème d’Euler: Si une fonction est homogène de degré \(r\), alors:

\[r f(x_1,x_2,...,x_n) = \sum_{i=1}^n \frac{\partial f}{\partial x_i}x_i.\]

À faire

Exercice E: Trouvez le degré d’homogénéité de la fonction \(f(x,y)=x^\alpha y^\beta\) des deux façons.

Approximation et maximum¶

\[\begin{split}f(x,y) \simeq f(x_0,y_0) + f'_x(x_0,y_0)(x-x_0) + f'_y(x_0,y_0)(y-y_0) \\ +\frac{1}{2}f''_{xx}(x_0,y_0)(x-x_0)^2 + \frac{1}{2}f''_{yy}(x_0,y_0)(y-y_0)^2 + \\ +f''_{xy}(x_0,y_0)(x-x_0)(y-y_0).\end{split}\]

Condition pour un maximum:

Nécessaire: \(f'_x(x,y)=0, f'_y(x,y)=0\)
Suffisante: \(\frac{1}{2}f''_{xx}(x_0,y_0)(x-x_0)^2 + \frac{1}{2}f''_{yy}(x_0,y_0)(y-y_0)^2 +f''_{xy}(x_0,y_0)(x-x_0)(y-y_0)<0\)

Voir aussi

La condition suffisante est reliée au déterminant du Hessien de la fonction (un concept qui nous n’utiliserons pas en classe, mais qui devrait rappeler des souvenirs).

Maximisation avec contrainte¶

Approche directe

Quand le problème prend la forme:

\[\begin{aligned} \max_{x,y} \{ f(x,y): g(x,y) \leq m\}\end{aligned}\]

Et qu’on peut inverser \(g(x,y)=m\) tel que \(y=q(x,m)\), alors la solution du problème contraint pour \(x\) est la même que celui de :

\[\begin{aligned} \max_{x} \{ f(x,q(x,m))\}\end{aligned}\]

La CPO est \(f'_x(x,q(x,m)) + f'_y(x,q(x,m))q'(x,m) = 0\). On peut résoudre pour \(x^*\) et utiliser \(y=q(x)\) pour trouver \(y^*\).

À faire

Exercice F: Maximisez la fonction \(f(x,y) = \log x + \log y\) sous la contrainte \(x+y \le m\).

Avec plusieurs variables et contraintes, cette approche n’est pas très pratique…

Le lagrangien

La méthode de Lagrange consiste à résoudre pour \((x,y)\),

\[\begin{split}\begin{aligned} f'_x(x,y) - \lambda g'_x(x,y) = 0 \\ f'_y(x,y) - \lambda g'_y(x,y) = 0 \\ g(x,y) = m\end{aligned}\end{split}\]

où \(\lambda\) est un multiplicateur de Lagrange.

Ces trois équations sont les CPO du lagrangien:

\[\begin{aligned} \max_{x,y,\lambda} L(x,y,\lambda) = f(x,y) - \lambda (g(x,y)-m)\end{aligned}\]

Le lagrangien \(L(x,y,\lambda)\) est une fonction objective modifiée qui permet de pénaliser la maximisation pour la contrainte (pour s’assurer qu’elle soit respectée). On remarque que si \(\lambda = 0\), on a les deux CPO non-contraintes \(f'_x(x,y)=0\) et \(f'_y(x,y)=0\) qui donnent une solution optimale sans avoir besoin de la troisième. Seulement si la contrainte est mordante (si \(\lambda \neq 0\)) aurons-nous une solution différente…

À faire

Exercice G: Maximisez la fonction \(f(x,y) = \log x + \log y\) sous la contrainte \(x+y \le m\) par la méthode du lagrangien.

Théorème de l’envelope¶

Considérons la fonction \(f(x,p)\) où \(p\) est hors de contrôle de l’agent qui optimise (exogène). On dénote:

\[V(p) = \max_x f(x,p) , \quad x^*(p) = \arg \max_x f(x,p)\]

La première fonction, \(\max\) retourne la valeur maximale de la fonction en choissant \(x\) et en gardant \(p\) constant. C’est une fonction qui dépend de \(p\) seulement (\(x\) a été choisi tel qu’il maximise la fonction). La deuxième retourne le \(x\) qui maximise \(f(x,p)\) en gardant encore une fois \(p\) constant. C’est donc une fonction de \(p\).

Un lien évident existe entre les deux \(V(p) = f(x^*(p),p)\). On peut utiliser ce lien pour étudier comment la valeur maximale de \(f\) change quand on change \(p\):

\[V'(p) = f'_x(x^*(p),p)x^{*'}(p) + f'_p(x^*(p),p)\]

On a par définition \(x^*(p)\) maximisant \(f(x,p)\). Donc, \(f'_x(x^*(p),p) = 0\) de par la CPO.

Ainsi, le premier terme de \(V'(p)\) est zéro.

On obtient \(V'(p) = f'_p(x^*(p),p)\).

Ceci implique que la dérivée de la valeur maximale par rapport à une variable exogène est la dérivée de la fonction objective par rapport à cette variable exogène, sans utiliser la règle de chaine (sans changer la solution optimale). C’est un raccourci (approximation) qui sera utile à plusieurs moments dans le cours.

À faire

Exercice H: Trouvez la forme de \(V'(p)\) pour la fonction \(V(p) = (10 - p\frac{x^*(p)}{2})x^*(p)\) où \(x^*(p) = \arg \max_x f(x,p)\) et \(f(x,p) =(10 - p\frac{x}{2})x\).

L’interprétation du multiplicateur

Il n’est pas nécessaire de résoudre pour la valeur de \(\lambda\) afin de trouver les valeurs optimales de \(x\) et \(y\). Mais, si on le fait, \(\lambda\) a une interprétation utile pour certaines applications que nous verrons.

Par le théorème de l’enveloppe, si

\[V(m) = \max_{x,y,\lambda} f(x,y) - \lambda (g(x,y)-m)\]

alors \(V'(m) = \lambda\). La valeur maximale augmente de \(\lambda\) quand on augmente (marginalement) \(m\) (quand on relâche la contrainte).

À faire

Exercice I: Démontrez dans le problème précédent (H) qu’une augmentation marginale de \(m\) a pour effet d’augmenter le maximum de \(\lambda\). Pour ce faire résoudre les CPO du lagrangien pour \(x,y,\lambda\), remplacez ces expressions dans \(f(x,y)\) et prendre la dérivée par rapport à \(m\). Montrez que cette dérivée est égale à la valeur de \(\lambda\).

Note sur les logarithmes¶

Note

Dans les notes, nous utiliserons \(\log\) en base \(e=2.718281828459\) et non en base 10. Donc, il s’agit du logarithme naturel (\(\ln = \log_e\)). Python utilise aussi la base exponentielle.