Le Travail¶
Le problème du choix du consommateur portait sur le panier de bien à consommer pour un revenu qui lui était exogène. Dans la réalité, notre revenu n’est pas exogène. On peut décider de travailler moins ou davantage, ce qui influence notre revenu. Quand on le fait, on sacrifie du temps de loisir, ou du temps en famille (à produire des biens et services), ce qui a un coût. Ainsi, il est opportun d’étudier ce choix. On peut alors se poser plusieurs questions intéressantes: est-ce que des garderies à contribution réduite favorise le travail des femmes?, comment aider les travailleurs expérimentés à travailler davantage?, quels seraient les effets d’un revenu minimum garantie sur le taux d’emploi?
Offre de Travail¶
Pour modéliser ce choix, nous allons introduire un nouveau bien, le temps de loisir \(L\). Le temps dans une journée (effectif en omettant le sommeil et soins personnels) est donné par \(T\). Ainsi, le temps de travail est \(H=T-L\). Içi, on suppose que les deux seules utilisations du temps sont le loisir et le travail. Il est possible d’introduire d’autres utilisations du temps. Le prix Nobel Gary Becker a été un des pionners dans l’analyse de l’allocation du temps.
Le consommateur à des préférences pour \((C,L)\), où \(C\) représente les dépenses de consommation (on normalise son prix à 1) et \(L\) le loisir compté en heures ou autre mesure du temps, représentées par la fonction d’utilité \(u(C,L)\), généralement concave dans ses deux arguments. Ainsi le TMS entre la consommation et le loisir est donné par:
et représente (en valeur absolue) la valeur accordée à une heure de loisir supplémentaire en termes de consommation. Ainsi, le loisir à une valeur positive.
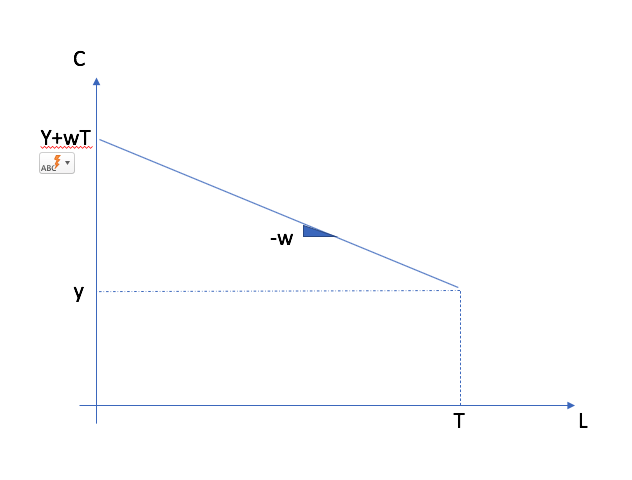
Quand il travaille, le consommateur a un salaire horaire de \(w\) et un revenu autre de \(y\). S’il travaille \(H=T\) heures, il a le revenu maximum de \(I = w T + y\) (en anglais, full income). Ses dépenses sont faites en termes de deux biens \(C\), sa consommation et \(L\) le loisir dont le coût d’opportunité par heures travaillées est de \(w\). Ainsi, la contrainte budgétaire est:
Fait intéressant à noter, le revenu de l’agent est maintenant fonction du prix du loisir \(w\). On peut écrire la contrainte, en notant que \(H=T-L\):
La contrainte budgétaire, dans l’espace \((C,L)\) est coudée dès suite de la présence de \(y\) et a une pente de \(-w\).
Le problème d’offre de travail peut donc être présenté sous la forme d’un lagrangien à maximiser:
Les CPO donnent:
La première condition stipule que la valeur absolue du TMS (la valeur d’une heure de loisir) doit être égale à son coût d’opportunité (\(w\)). La deuxième condition est la contrainte budgétaire. La solution de ce système de deux équations donne en particulier \(L^*(w,y)\), la demande marshalienne du loisir. L’offre de travail est donnée par \(H^*(w,y) = T - L^*(w,y)\).
Exercice A: Trouvez la demande de loisir et l’offre de travail pour \(u(C,L) = C^{\alpha}L^{1-\alpha}\).
Le multiplicateur de Lagrange se fait donner l’interprétation de l’utilité marginale du revenu (on peut le vérifier par le théorème de l’enveloppe). Par ailleurs, il est aussi important de noter que la présence de \(y\) peut faire en sorte qu’une solution de coin est probable, où \(L^* = T\), et le TMS est plus grand que le salaire horaire.
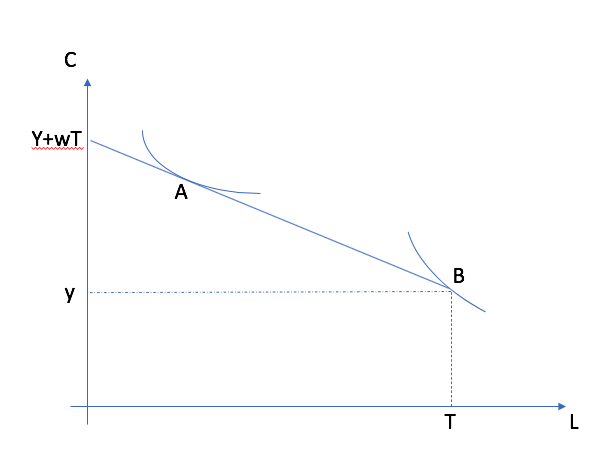
La situation A montre un choix d’heures travaillées élevées alors que la situation B montre une situation où l’individu ne travaille pas car dans une solution de coin. Dans ce cas, le TMS est plus grand que le salaire à \(L=T\).¶
Le modèle d’offre de travail classique est très simple et peut être bonifié dans plusieurs directions. Une direction souvent prise est de permette un choix restreint d’heures travaillées. En effet, il est souvent difficile pour un travailleur de choisir exactement le nombre d’heures qu’il aimerait travailler. Ces considérations sont importantes pour prédire l’effet de différentes politiques.
Effets Substitution et Revenu¶
La présence de \(w\) dans le revenu maximal complique l’analyse d’un changement de salaire. En effet, un salaire qui augmente veut maintenant dire que le coût d’opportunité du loisir augmente (effet substitution), mais le revenu maximal augmente aussi, ce qui fait que le consommateur peut se permettre davantage de loisirs (si le loisir est un bien normal).
Pour comprendre ces effets, notons d’abord que le modèle ici haut est en fait seulement fonction d’une variable, on peut substituer la contrainte budgétaire dans le problème de sorte que le problème dépend seulement du loisir:
La condition de premier ordre est :
où \(u_C\) est l’utilité marginale de la consommation et \(u_L\), l’utilité marginale du loisir. En prenant la différentielle totale, en fixant \(dy=0\), on obtient,
où \(\Delta\) est un terme négatif si la solution n’est pas de coin (en fait la valeur de la dérivée seconde à la solution). Ainsi l’effet d’un changement de salaire sur le loisir est la somme d’un effet négatif (premier terme) et d’un deuxième terme positif si le loisir est un bien normal. Ainsi, l’effet d’une hausse de salaire sur le loisir est indéterminé et dépendra de la force relative de ces deux effets.
On peut montrer que le premier terme est en fait l’effet substitution (ou compensé), \(\frac{d L}{d w}|_{dU=0}\). Le deuxième terme est l’effet revenu.
On peut écrire en termes d’offre de travail pour obtenir l’équation de Slutsky d’offre de travail:
L’effet d’une hausse de salaire est la somme d’un effet substitution (compensé) positif et d’un effet revenu négatif (si loisir est un bien normal). En termes d’élasticité, on peut écrire:
On peut estimer les élasticités salaire et revenu de différentes façons. Par exemple, Imbens et al. (2001) ont estimé l’effet de gagner la loterie sur l’offre de travail des gagnants. Ceci nous renseigne sur \(\eta_{Y}\). Ils trouvent une élasticité des revenus de travail de -0.05 à -0.1 de gagner la loterie.
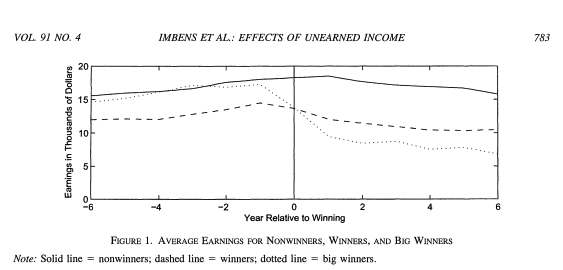
Imbens et al. (2001)¶
Concernant l’élasticité salaire, la littérature est vaste, et utilise un nombre important de méthodes. Généralement, l’élasticité est faible pour les hommes, plus forte pour les femmes, particulièrement pour ce qui est du choix de travailler ou non.
Exercice B: Trouvez les élasticités salaire et salaire compensé pour \(u(C,H) = C - \frac{H^{1+\frac{1}{\epsilon}}}{1+\frac{1}{\epsilon}}\).
Il est possible qu’une hausse de salaire horaire réduise l’offre de travail. Cet effet contre-intuitif est pourtant présent dans certaines professions. Un exemple souvent donné est celui des médecins au Québec qui ne semblent pas avoir augmenté leur offre de travail après l’énorme augmentation salariales consentie à la fin des années 2000. La part des médecins travaillant à temps partiel a aussi augmenté considérablement.
Question pour discussion: Dans l’optique d’augmenter les services à la population, devrait-on augmenter ou diminuer la rémunération à l’acte des médecins?
Il est aussi possible que les individus visent un revenu cible (income targeting), et donc qu’ils ne réagissent pas à une hausse de salaire comme on pourrait se l’imaginer. Cette étude sur les chauffeurs de taxi à New York en est un bon exemple. Le income targeting est un cas spécial de l’équation de Slutsky où les effets substitution et revenu s’annulent.
La Taxation¶
La taxation peut prendre plusieurs formes. Dans sa forme la plus simple, il s’agit d’un taux d’imposition \(\tau\) sur les revenus de travail. Si on regarde la contrainte budgétaire, on a :
Ainsi, l’augmentation d’une taxe est similaire à une diminution du salaire, ce qui mène à une perte de bien-être. Puisqu’on sait que l’effet d’une baisse de salaire est indéterminé sans connaître les préférences exactes, il n’est pas possible de dire si une augmentation de l’imposition réduit l’offre de travail.
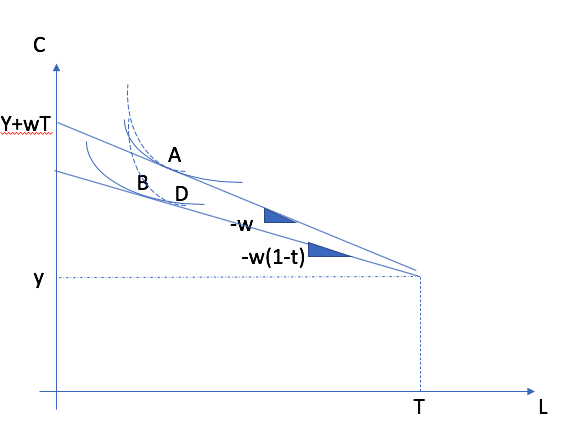
Par rapport à une situation de référence A, l’effet de la taxe dépendra de la forme des courbes d’indifférences. Il est possible que le travailleur travaille moins (situation D, effet substitution domine) ou davantage (situation B, effet revenu domine).¶
De plus, l’implémentation de la taxe est importante. Plus elle est permanente, plus les travailleurs auront un effet revenu élevé tandis que si la taxe est transitoire, seul l’effet substitution sera à l’oeuvre. Finalement, si l’impôt est compensé pour certains ménages, c’est l’effet compensé qui devrait être utilisé pour estimer l’effet de la taxe sur les comportements de ces ménages. Ces subtilités compliquent l’analyse des effets désincitatifs de la taxation. Ainsi la question à savoir si la taxation est un désincitatif au travail n’est pas simple…
Exercice C: Dans le cas où les préférences sont données par \(u(C,H) = C - \frac{H^{1+\frac{1}{\epsilon}}}{1+\frac{1}{\epsilon}}\), trouvez l’effet d’une taxe \(\tau\) sur l’offre de travail et la perte de bien-être associée à la taxation.
Dans les faits, le système fiscal ne peut être résumé à un taux d’imposition uniforme, \(\tau\). D’abord, l’impôt est progressif et le taux change par palier d’imposition. Par ailleurs, des crédits d’impôt affectent le taux effectif d’imposition parce qu’ils sont fonction du revenu de travail (e.g. prime au travail québécoise, crédit pour frais de garde). Donc, plus généralement, les impôts à payer sont donnés par: \(\tau(wH,y)\) qui dépend de la source des revenus et est généralement non-linéaire dans ces revenus.
Une mesure du taux de taxe effectif est le taux effectif marginal d’imposition ou TEMI. Sa formule est donnée par:
Le TEMI est très utile pour mesurer l’impôt effectif payé sur un changement d’heures \(\Delta H\). Pensons au travailleur d’usine qui doit décider s’il fait des heures supplémentaires. Il se peut que son revenu net augmente de très peu quand les heures travaillées augmentent. Dans l’exemple Python, vous allez calculer ces taux pour le cas d’un individu au Québec.
Une méthode intéressante pour estimer les effets de la taxation est de voir si les individus restreignent de manière volontaire leurs revenus de travail afin de se situer juste en dessous des changements de taux d’imposition des paliers. L’étude américaine de Saez (2010) est une application de cette méthode dite de bunching. Ils trouvent une forme de dancing au premier palier, mais aucun bunching aux autres paliers.
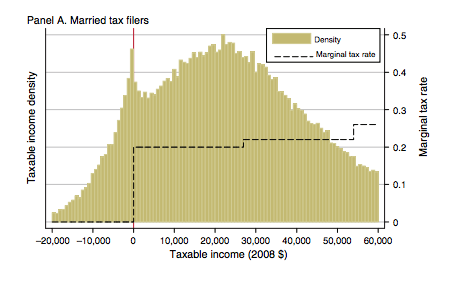
Saez (2010)¶
Transferts¶
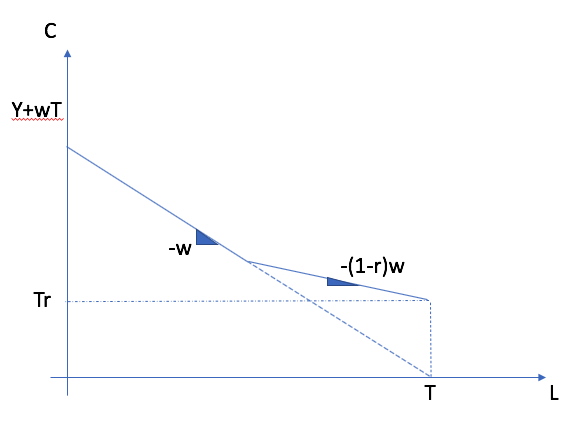
Les gouvernements procurent souvent des transferts aux individus avec des revenus faibles. Ces transferts agissent comme les revenus autres \(y\). Donc a priori, ils n’ont qu’un effet revenu sur l’offre de travail et donc peuvent augmenter la probabilité d’une solution de coin surviennent (offre de travail de zéro).
Par ailleurs, ils peuvent aussi mener à des effets substitutions s’ils sont récupérés en fonction des revenus de travail. Dans les faits, les gouvernements ne peuvent procurer à tous les individus, qu’ils soient riches ou pauvres un revenu minimum inconditionnel. Ainsi, les transferts sont généralement réduient en fonction des revenus de travail.
Par exemple, l’aide sociale au Québec est réduite dollar pour dollar (donc 100% de taxe implicite). La prime au travail augmente d’abord avec les revenus pour ensuite être récupérée. Le supplément de revenu garanti est récupéré à un taux au-delà de 50% pour les travailleurs âgés.

Source: Rapport final, Comité sur le revenu minimum garanti, Volumne 2.¶
En terme graphique, on se retrouve donc avec une contrainte budgétaire qui coudé, parce qu’à un certain point, le transfert est complètement récupéré.
Si l’effet substitution domine, ceci a pour effet de réduire encore plus l’offre de travail et créer ce qu’on appelle souvent une trappe de la pauvreté, i.e. la personne qui reçoit des transferts n’a pas beaucoup d’incitatifs à sortir de cette situation. Les bougons, personnages de la populaire série, évoquent souvent cette trappe pour justifier leur recours à l’aide sociale.
Question pour discussion: Pour ou contre un revenu minimum garanti, en particulier pour sortir les gens de la pauvreté?
Matériel pour discussion:
Rapport du comité d’experts sur le revenu minimum garanti.