Bien-être¶
Pour bien évaluer une politique, on peut regarder son efficacité, c’est-à-dire cible-t-elle le groupe visé, est-ce qu’elle a l’effet attendu sur les comportements, et combien coûte-t-elle étant donné son efficacité?
Par exemple, une réglementation sur la qualité de l’air peut inciter plusieurs individus à changer de comportement. Le coût par unité d’amélioration de la qualité de l’air peut être élevé. Comment statuer si la politique est désirable?
En général, la qualité de l’air est valorisée par la population. Donc, on peut mesurer les bénéfices par les préférences. Au final, on peut savoir si la réglementation est bénéfique étant donné son coût. Alors qu’on s’arrête souvent aux retombées économiques ou fiscales d’une intervention, on oublie très souvent de compter les bénéfices en termes de bien-être.
Afin de répondre à ces question, et permettre de juger des politiques, il faut aller une étape plus loin que ce qu’on a fait et se demander comment on peut mesurer le bien-être par les préférences.
Trois approches existent: une approche utilitarienne, une approche hicksienne et finalement une approche du bonheur rapporté.
Utilisarisme¶
Pour chaque citoyen \(i\in \{1,\ldots,N\}\), on peut construire une fonction d’utilité \(U_i\) qui représente ses préférences sur pour un panier de bien dans un ensemble \(B\). Supposons que chaque citoyen obtient le panier \(B_1\), \(B_2\), …, \(B_N\). Selon cette approche une mesure d’un bien-être est
Si on utilise ce critère de bien-être, alors une politique \(\mathcal P_0\) est mieux que l’alternative \(\mathcal P_1\) si la somme des utilités est plus élevée. Ici la fonction qui agrège les utilités des différents citoyens est linéaire, tel que proposé par Bentham, mais on peut aussi généraliser à d’autres formes, par exemple l’utilité minimale sous-jacente à la théorie de la justice sociale de (Rawls).
Cette approche est problématique et peu utilisée. Elle suppose des utilités cardinales alors que les utilités sont ordinales… On se rappelle que \(U_1\) représente les préférences du citoyen \(1\), mais \(f(U_1)\) représente les mêmes préférences pour n’importe quelle fonction croissante \(f\). Il existe un nombre infini de fonctions d’utilités qui représentent les mêmes préférences. Par exemple, on aurait pu prendre \(2\times U_1\), ce qui peut affecter le choix de politique si une politique favorise davantage ce citoyen…
Donc, le classement des politiques est ambigu: on peut avoir \(\mathcal P_0\) meilleure si \(W = U_1 + U_2\) alors que \(\mathcal P_1\) est meilleure si on utilise \(W = 2U_1 + U_2\)
En somme, le bien-être devrait dépendre des préférences et non de \(U\). Il demeure que sans trahir l’ordinalité des préférences, les utilités demeurent utiles. On peut définir par exemple une amélioration au sens de Pareto, si l’utilité de tous les individus est au moins égale au niveau de référence avec un changement de politique. Si personne ne perd, et que certains gagnent, cette situation peut être considérée meilleure au sens de Pareto. L’amélioration au sens de Pareto est indépendante de l’échelle de l’utilité. C’est un concept ordinal.
Variation compensatoire¶
Une approche plus prometteuse est de quantifier de façon monétaire le bien-être à l’aide des préférences. John Hicks propose d’utiliser la variation compensatoire.
Qu’est-ce qu’une politique dans le problème du consommateur? Une politique \(\mathcal P\) défini une contrainte budgétaire \(C_i(\mathcal P,I_i)\) pour le citoyen \(i\) (où \(I_i\) est le revenu).
On peut utiliser l’utilité indirecte comme point de départ. L’utilité maximale du citoyen \(i\) étant donné sa contrainte est:
\[U_i^*(\mathcal P,I_i) = \max_{B \in C_i(\mathcal P, I_i)} U_i(B)\]
Exemple: Deux biens \(X\) et \(Y\). Utilité \(U(X,Y) = \log X + \log Y\). Une politique \(\mathcal P\): avec une taxe multiplicative \(\tau\) sur le prix de \(Y\). Alors l’utilité indirecte est donnée par:
Dénotons \(\mathcal P_0\) le statu quo et considérons l’implémentation de la politique \(\mathcal P\). On peut définir la variation compensatoire comme étant le montant \(\Delta I^{CV}\) tel que
\[U^*(\mathcal P_0,I) = U^*(\mathcal P,I - \Delta I^{CV})\]
C’est le montant qu’on doit retirer au consommateur pour garder son bien-être constant au niveau du statu quo.
Note: on utilise une convention de signe telle que \(\Delta I^{CV}>0\) quand le changement de politique est bénéfique. Par exemple, une baisse de taxe, une hausse des transferts, une baisse de prix.
Exercice A: Trouvez l’expression de la variation compensatoire pour \(U = XY\) et une taxe \(\tau\) sur le bien \(Y\).
\(\Delta I^{CV}\) dépend seulement des préférences
\[\begin{split}U^*(\mathcal P_0,I) = U^*(\mathcal P, I - \Delta I^{CV}) \\ \Rightarrow 2 U^*(\mathcal P_0,I) = 2 U^*(\mathcal P, I- \Delta I^{CV})\end{split}\]
De manière générale, pour n’importe quelle fonction \(f\),
\[\begin{split}U^*(\mathcal P_0,I) = U^*(\mathcal P, I - \Delta I^{CV}) \\ \Rightarrow f[U^*(\mathcal P_0,I)] = f[ U^*(\mathcal P, I - \Delta I^{CV})]\end{split}\]
Cas spécial utile¶
Considérons les préférences pour un bien \(X\) et l’argent \(Y\). Les préférences sont représentées par \(U(X,Y) = V(X) + Y\).
La politique de référence est \(\mathcal P_0\). Le consommateur choisi l’allocation \((X_0, Y_0)\). Maintenant, considérons un changement \(\mathcal P\). Le nouveau choix optimal est \((X_1, Y_1)\).
Dans ce cas, la variation compensatoire est \(\Delta I^{CV}\) ou
La variation compensatoire est égale au changement de l’utilité. De par la linéarité dans l’argent, l’utilité est en dollars. Le TMS de cette fonction d’utilité est:
Puisque \(p_Y=1\) dans le cas où \(Y\) est de l’argent, \(V'(X)\) représente la disposition à payer (en dollars) pour une unité de \(X\).
Surplus du consommateur¶
Supposons le cas de préférences représentées par l’utilité quasi-linéaire pour le bien \(X\) et l’argent \(Y\). \(U(X,Y) = V(X) + Y\). Supposons que \(V\) est concave (\(dV/dX\) diminue en \(X\)).
Considérons une situation où le bien \(X\) ne peut être acheté \(\mathcal P_0\) et une alternative où \(\mathcal P\) permet d’acheter le bien \(X\) au prix \(p_X\). Le problème est donné par
On peut substituer la contrainte pour obtenir \(\max_{X} V(X) + I - p_X X\). La CPO est
Ce qui permet de trouver la demande \(X^*(p_X)\). Dénotons \(p_X(X^*) = \frac{dV}{dX}\), la fonction de demande inverse. Ainsi un point sur cette demande inverse donne la disposition à payer pour une unité de \(X\).
Dans le cas d’un nouveau produit, la variation compensatoire de \(\mathcal P_0\) à \(\mathcal P\) est le surplus du consommateur.
Le premier terme n’est rien d’autre que l’aire sous la courbe de la fonction de demande inverse:
C’est la somme des dispositions à payer pour chaque unité de \(X\). Le deuxième terme est le coût d’acheter la quantité \(X^*\). Le surplus provient du fait que le consommateur valorise chaque unité qu’il achète au prix \(p_X\) davantage que le prix \(p_X\).
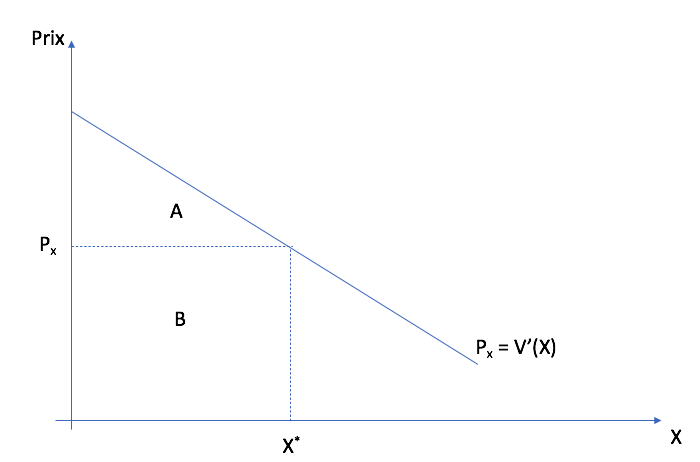
La zone A+B est donnée par \(V(X^*) - V(0)\) alors que la zone B est la dépense \(p_{X}X^*\). Ainsi le surplus du consommateur est A+B - B = A.¶
Exercice B: Si \(V(X) = 10 X - \frac{1}{2}X^2\), trouvez l’expression du surplus du consommateur.
Bien-être et taxation¶
La taxation affecte le prix payé par le consommateur. Donc, elle a des effets sur le bien-être. Dans la théorie du consommateur, nous avons déjà vu qu’une hausse de prix réduit le bien-être du consommateur. Nous avons qu’à appliquer le concept de revenu compensé à l’analyse des taxes.
Considérons l’élimination d’une taxe, le prix passant de \(p_X = p+t\) à \(p_X = p\) . On a \(X^*(p) > X^*(p+t)\) (le bien n’est pas Giffen). Le revenu de la taxe est \(T= t X^*(p+t)\). Quand le gouvernement collecte une taxe, il faut implicitement faire comme si les revenus seront redistribués de manière forfaitaire. Du point de vue du bien-être, l’argent collecté par le gouvernement n’est pas perdu…
En termes de variation compensatoire, on a
\[\Delta I^{CV} = U[X^*(p), I - pX^*(p)] - U[X^*(p+t), I - (p+t) X^*(p+t)] > 0\]
On obtient que \(\Delta I^{CV} > T\): Le consommateur est prêt à payer un montant supérieur au revenu généré par la taxe pour le gouvernement. Donc, l’élimination de la taxe lui est bénéfique.
Le gain de bien-être associé à l’élimination de la taxe est donc \(\Delta W = \Delta I^{CV} - T\). Pourquoi le \(T\) est soustrait? En enlevant la taxe, le gouvernement ne peut plus distribuer de manière forfaitaire les revenus de la taxe. Donc, il faut l’enlever du changement de surplus du consommateur. Si on introduit une taxe, on a plutôt, \(\Delta W = \Delta I^{CV} + T\) parce qu’on doit redistribuer de manière forfaitaire les revenus de la taxe, ce qui est un gain pour le consommateur.
Exercice C: Si \(V(X) = 10 X - \frac{1}{2}X^2\), trouvez la perte de bien-être associée à une nouvelle taxe \(t\) sur le bien \(X\). Montrez graphiquement cette perte.
Bien-être et environnement¶
Généralement, on accorde une valeur positive à la qualité de l’air.
Il n’y a pas de marché pour la qualité de l’air. Avec le Clean Air Act (1977), le gouvernement américain a mis en place un nombre important de mesures pour réduire la pollution. Les lois sont couteuses à implémenter et faire respecter. Pour justifier ces lois, on doit montrer que les bénéfices sont élevés.
Considérons un changement de politique \(\mathcal P_0\): aucun contrôle, aucun coût, à \(\mathcal P\): contrôle de la pollution, ce qui implique des coûts. La variation compensatoire devrait être positive si les citoyens valorisent la qualité de l’air.
Empiriquement, comment faire pour estimer les préférences?
On peut trouver une situation où des gens ont dû faire un arbitrage entre pollution et leur richesse financière. Par exemple, l’achat d’une maison dépend bien sûr du prix, mais aussi de l’environnement, etc. Les prix et la qualité de l’air varient à l’intérieur d’une ville. Dans un marché, les prix devraient être plus élevés quand la qualité de l’air est plus élevée si les acheteurs valorisent la qualité de l’air.
En utilisant des données provenant de transactions immobilières, on peut déterminer la valeur accordée à la qualité de l’air. Définir \(X\) comme étant mesure de la qualité de l’air, (e.g. concentration de particules) On peut postuler une fonction d’utilité quasi-linéaire:
Avec cette fonction d’utilité \(V'(X)\) représente la disposition à payer pour la qualité de l’air. En régressant le prix des transactions sur \(X\) et en contrôlant pour d’autres facteurs affectant le prix des transactions, on obtient un estimé de \(V'(X)\).
Chay et Greenstone (2005) obtiennent des estimés de l’élasticité prix-particule (entre -0.2 et -0.35).
Maintenant, comment évaluer une politique avec ces informations? Le gouvernement dépense \(X_{GOV}\). Le coût pour financer ces dépenses est \(c X_{GOV}\) avec \(c>1\) est le coût incluant la perte de bien-être dû à la taxation nécessaire.
La politique change de \((0,0)\) à \((X_{GOV}, - c X_{GOV})\). Le surplus du consommateur est la variation compensatoire:
Une fois l’analyse faite, on peut aussi se demander quelle serait la qualité de l’air optimale afin de voir s’il est encore possible de resserrer les restrictions.
La pollution optimale est le niveau de pollution qui maximise:
La CPO est
\[\frac{dV}{d X}_{|X^*} = c\]
Il est donc possible de quantifier ceci une fois tous les paramètres connus.
Exercice D: Pollution par le bruit. L’élasticité prix des maisons à la pollution par le bruit est -0.2. Le gouvernement considère réduire le niveau de pollution de 10% près d’une autoroute. Les ingénieurs nous disent que la technologie nécessaire coûtera 1000$ pour chaque propriété. La politique est financée par une taxe qui mène à une perte de bien être de 43 cents pour chaque dollar à financer. Est-ce que cette politique augmente le bien-être?
Cette approche est très utilisée. Même si a priori, ces problèmes semblent dépendre de la spécification des préférences, ce n’est pas toujours le cas, comme le montre l’exercice D (on a besoin que de l’élasticité prix dans l’exercice). Un autre enjeu est la possibilité que certains aient une variation compensatoire négative alors que pour d’autres celles-ci sont positives. À moins de spécifier un mécanisme pour agréger les variations compensatoires (une somme?), ce qui n’est pas neutre d’un point de vue de l’équité, l’approche la plus commune sera de parler d’amélioration potentielle de Pareto si la somme des variations compensatoires est positive et une forme de compensation pourrait être prévue pour ceux qui y perdent. La plupart des politiques font des perdants. Il est donc tout aussi important de statuer sur la désirabilité de la politique que d’identifier les perdants afin de les compenser.
Approche bonheur rapporté¶
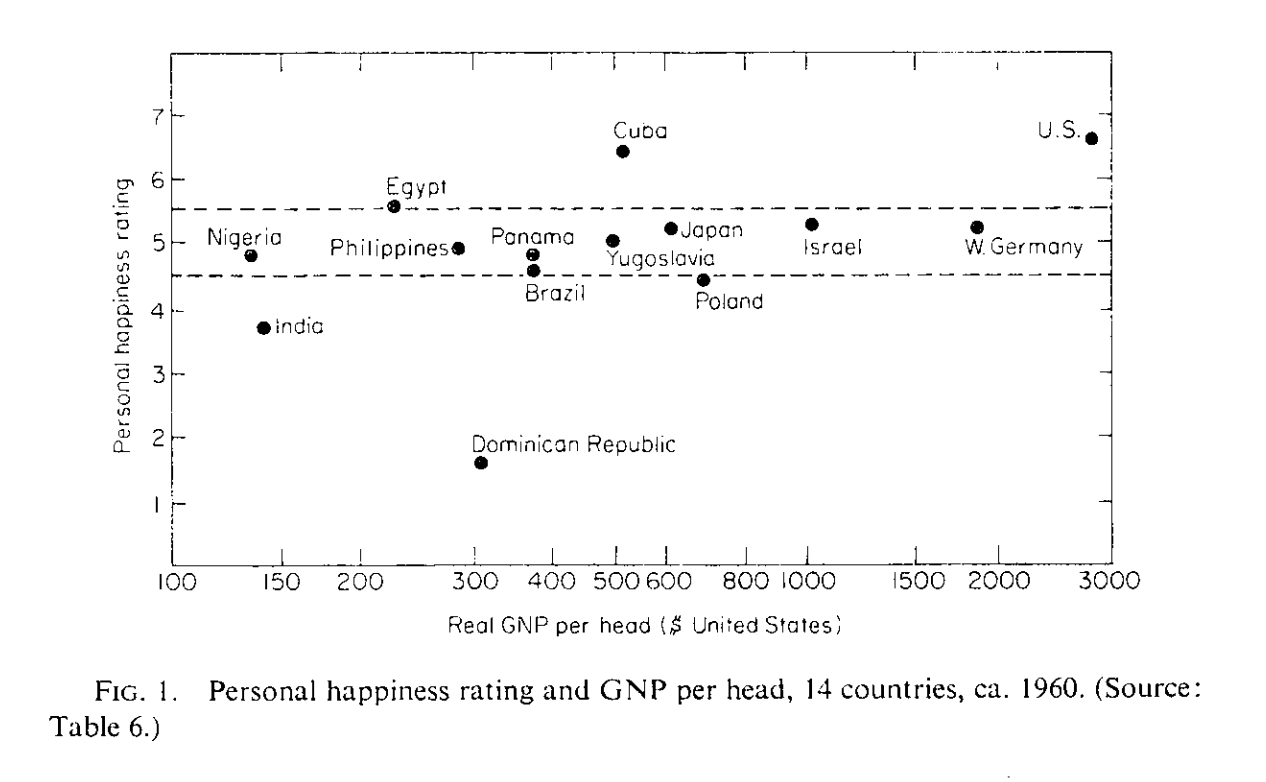
Pourquoi ne pas simplement demander aux gens s’ils sont heureux? Sur une échelle allant de 1 à 10, êtes-vous heureux? Ceci évite d’avoir à spécifier les préférences. C’est une approche qui gagne une certaine crédibilité avec le budget 2019 en Nouvelle-Zélande. C’est Richard Easterlin qui a beaucoup popularisé l’utilisation de mesures directes du bien-être. Le Paradox de Easterlin a longtemps suscité de l’intérêt:
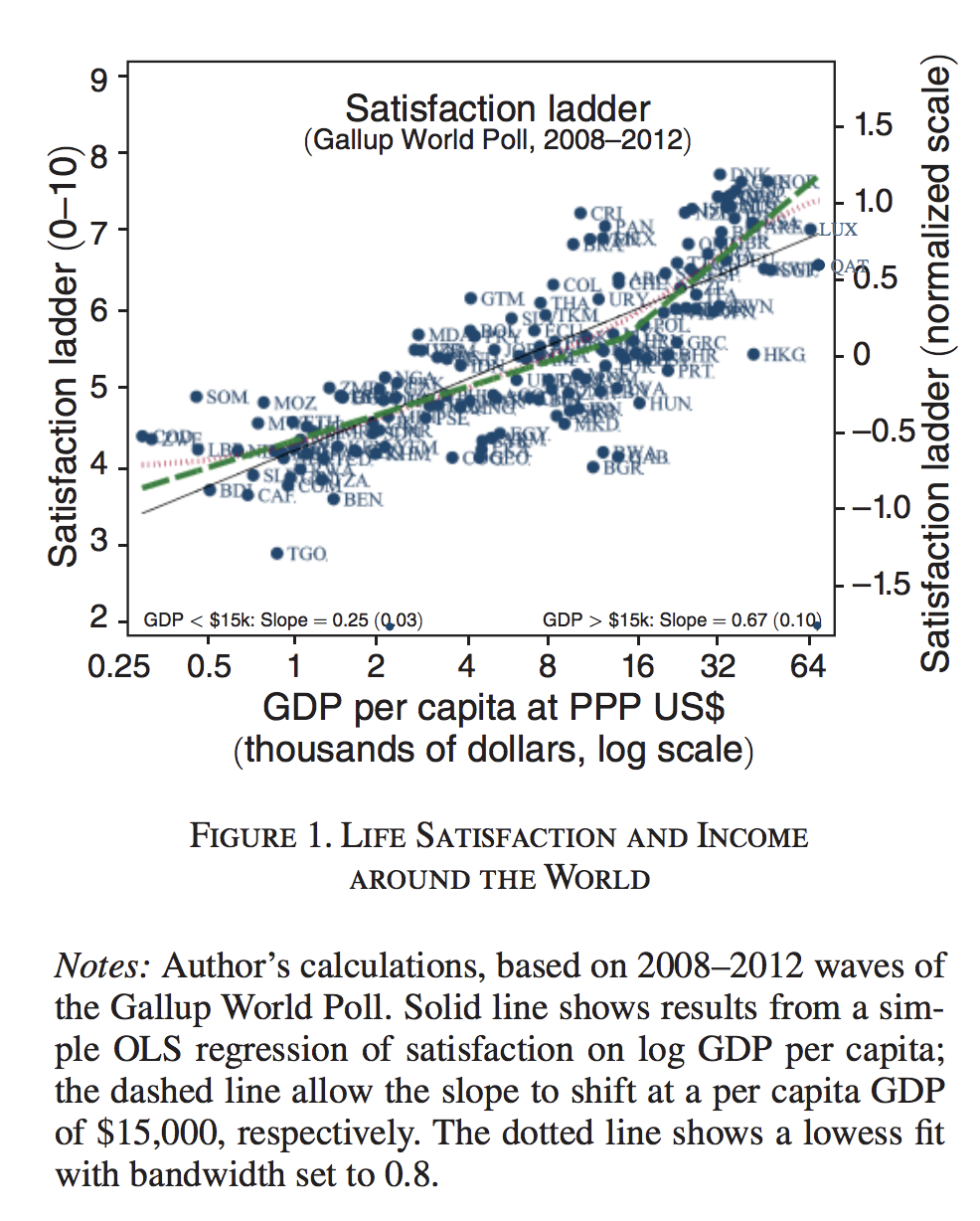
Donc, on ne serait pas plus heureux avec davantage de revenus, un résultat contre-intuitif: l’argent ne fait pas le bonheur. Mais plus tard, on a montré que ce Paradoxe ne tenait plus:
Il n’en demeure pas moins, que ces mesures peuvent être utiles puisque le bonheur, c’est plus qu’un portefeuille bien garni. Pourquoi ne pas utiliser les mesures directes du bien-être pour évaluer les politiques?
Avantages: méthode directe sans avoir besoin d’un modèle qui prend en compte toutes les dimensions du bien-être.
Inconvénients: On peut mesurer le bien-être de différentes façons et les gens ont des manières différentes de répondre. Plusieurs biais psychologiques en jeu.
Très peu d’études utilisent ces mesures pour évaluer des politiques. Mais il y a beaucoup d’intérêt, pour de bonnes raisons.
Pour ceux qui veulent approfondir, voici une entrevue avec Angus Deaton sur la mesure du bonheur: