Asymétrie d’information

Information imparfaite

Akerlof (1970) a écrit un texte qui a changé à jamais la façon d’aborder les marchés quand il y a des problèmes d’information. Dans The Market for Lemons: Quality Uncertainty and the Market Mechanism, il démontre les conséquences dévastatrices sur l’équilibre de marché quand la qualité d’un produit varie et que cette qualité n’est pas observable.

lemons

Dans un article très intéressant, Gans et Shepherd (1994) rapporte que l’article fut très difficile à publier. En voici un extrait:

Citation

George Akerlof’s seminal contribution to the economics of information, « The Market for “Lemons”: Quality, Uncertainty and the Market Mechanism, » considered whether markets would exist if product quality were unobservable. Before the Quarterly Journal of Economics finally accepted Akerlof’s paper four years after he first sought to publish it, three journals called it a lemon. « I submitted it in June, 1967 to the American Economic Review. I got a reply from the editor which said that the article was interesting but the American Economic Review did not publish such trivial stuff. » The article next went to the Journal of Political Economy. Again it was rejected. Although the AER editor had refused the article because it was trivial, the JPE referee’s report asserted the opposite: that the paper was too general to be true. « It seemed to give a universality to my paper that was never intended. It said amongst other things that eggs came in different qualities, but they were graded and then traded. Didn’t “The Market for “Lemons » predict that no markets would occur at all if there were quality differences? Thus, in the view of this referee my paper predicted too much. Perhaps he forgot that the paper predicted the nonexistence of many markets which do not, in fact, exist. » Akerlof kept trying. « I next sent the article to the Review of Economic Studies. I had been urged by one of its co-editors to do that. Instead it went to another editor whose view of “The Market for “Lemons » was decidedly less favorable. It was rejected on the grounds again that it was “trivial.” Finally I sent it to the QJE which accepted it with some degree of enthusiasm.

Nous construisons ici un modèle simple qui démontre le résultat important de Akerlof.

Supposons que la qualité d’un bien \(q\) est représentée sur un continuum de 0 à 1. La qualité est distribuée de manière uniforme dans l’intervalle. Pour une variable aléatoire uniforme sur un intervalle \([0,b]\), la moyenne est donnée par \(b/2\). Ainsi la qualité moyenne est donc de \(1/2\).

On suppose aussi qu’il y a plusieurs acheteurs avec une disposition à payer \(v=\frac{3}{2}q\). L’utilité de ces derniers est \(v-p\). Il y a plusieurs acheteurs.

Les vendeurs ont un coût marginal égal à \(q\). Ils sont donc prêts à vendre leur voiture d’une qualité \(q\) à un prix \(q\).

Information parfaite

En information parfaite, il existe un prix \(p\) pour chaque niveau de qualité entre \(q\) et \(\frac{3}{2}q\). L’équilibre compétitif est \(p=q\) et donc le prix moyen et la quantité moyenne sont 1/2.

Information imparfaite

Maintenant, supposons que \(q\) n’est pas observable. Un acheteur peut espérer la qualité moyenne sur le marché. Ainsi sa disposition à payer est \(v=\frac{3}{2}\overline{q}\) où \(\overline{q}\) est la qualité moyenne sur le marché.

Quel est le prix d’équilibre? Pour un \(p\) donné, on peut trouver qui est prêt à offrir le bien. Rappelons que le coût marginal est \(q\). Ainsi tous les vendeurs avec \(q\leq p\) veulent offrir le bien à ce prix. Tous ceux avec \(q>p\) ne veulent pas l’offrir.

Par conséquent, puisque la qualité est distribuée de façon uniforme sur l’intervalle \(\left[0,p\right]\) la qualité moyenne est \(p/2\). Donc, \(\overline{q}(p)=p/2\).

Sachant ceci, l’acheteur voudra acheter si \(v>p\). Mais \(v\) est donné par

\[\frac{3}{2}\overline{q}(p)=\frac{3}{4}p<p\]

Ainsi, au prix \(p\), personne ne veut acheter du bien. Ceci est vrai pour tout \(p\). Il y a écroulement complet du marché et rien ne sera vendu en équilibre. C’est un résultat dramatique, mais qui démontre l’effet de l’information imparfaite. Il y a une perte de bien-être énorme parce que des biens qui ont une valeur supérieure au coût marginal ne sont pas vendus.

Un mécanisme d’antisélection est à l’oeuvre dans cet exemple. Tout prix qui est intéressant pour le propriétaire d’un bien de qualité \(q\) est encore plus intéressant pour le propriétaire d’un bien de mauvaises qualité \(q^{*}<q\). Ainsi il y a anti-sélection, ceux qui offrent le bien à un prix \(p\) ont parmi eux une surreprésentation de biens de mauvaise qualité (ceux de bonne qualité ne sont pas sur le marché).

Par la réglementation, le gouvernement peut imposer un système de certification de la qualité, ou une qualité minimale. Il peut aussi donner des recours aux acheteurs de biens de mauvaise qualité.

L’antisélection

Dans un contexte d’assurance, l’assureur ne peut généralement observer complètement le risque de chaque assuré. Au prix que l’assureur offrira, les risques les plus élevés sont plus susceptibles d’acheter l’assurance. Ainsi, l’assureur devrait augmenter sa prime pour ne pas faire de perte. S’en suit encore une perte des clients à plus faible risque qui contractaient l’assurance. La spirale destructrice de Akerlof peut se mettre en place. Il y a moyen de transposer ce cadre dans une analyse d’offre et de demande classique. Supposons que la demande inverse pour un produit d’assurance, par exemple, l’assurance maladie est donnée:

\[\pi(q) = D_0 - \alpha q\]

où \(\pi\) est la prime d’assurance et \(q\) est le nombre de personnes assurées. Parce que les individus ayant un risque inobservable plus élevé sont ceux qui coûtent plus cher à l’assureur, mais ont une disposition plus élevée à acheter l’assurance, le coût marginal pour l’assureur augmente dans la prime \(\pi\). Plus la prime augmente, plus le risque moyen augmente parmi ceux qui achètent l’assurance. Supposons une courbe de coût marginal donnée par

\[c(\pi) = C_0 + \beta \pi\]

avec \(\beta<1\) et \(C_0<D_0(1-\beta)\).

En termes de \(q\), on a :

\[c(q) = (1-\beta)C_0 + \beta (D_0 - \alpha q) = (1-\beta)C_0 + \beta D_0 - \beta\alpha q\]

La prime qui est optimale au sens de Pareto est celle telle que le coût marginal est égal à la disposition à payer marginale… Ainsi, on obtient:

\[\begin{split}\begin{aligned} D_0 - \alpha q =& C_0 + \beta D_0 - \alpha\beta q \\ q^* =& \frac{(1-\beta)D_0 - C_0}{\alpha(1-\beta)} \end{aligned}\end{split}\]

Que se passe-t-il en équilibre de marché? Si le risque est observable, on aura le même résultat que l’optimum de Pareto puisque les conditions du 1er théorème du bien-être s’appliquent. L’équilibre de marché est un optimum de Pareto. Par contre, la situation où les assureurs n’observent pas le risque est bien différente. Les assureurs en compétition opèrent au point où la prime est égale au coût moyen (elles ne font pas de profits ainsi…). Quel est le coût moyen? D’abord le coût total est donné par

\[C(q) = \int_0^q (C_0 + \beta(D_0-\alpha s)) ds = (C_0 + \beta D_0) q - \frac{\alpha\beta}{2}q^2\]

Donc, le coût moyen est:

\[AC(q) = C_0 + \beta D_0 - \frac{\alpha\beta}{2}q\]

Le coût moyen décroit dans le nombre de personnes assurées. Les premières personnes assurées sont celles qui ont le coût marginal le plus élevé alors que celles ayant un coût plus faible sont les dernières à s’assurer.

On a donc un équilibre de marché quand la prime est égale au coût moyen (alors profits nuls pour les assureurs):

\[\begin{split}\pi(q) = AC(q) \\ D_0 - \alpha q = C_0 + \beta D_0 - \frac{\alpha\beta}{2}q \\ \hat{q} = \frac{(1-\beta)D_0 - C_0}{\alpha(1-\frac{\beta}{2})}\end{split}\]

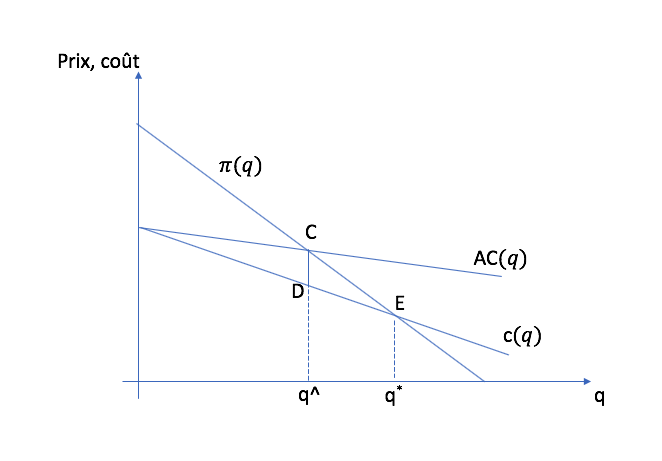
On remarque que \(\hat{q} < q^*\). Ainsi, l’antisélection réduit le nombre de personnes assurées. La prime d’équilibre est aussi plus élevée.

einav

La perte de bien-être vient du fait que des gens qui devraient être assurés ne le sont pas parce que l’assureur anticipe correctement qu’une baisse de prime entraine l’arrivée des mauvais risques, ce qui lui ferait faire une perte. La perte de bien-être est mesurée par le triangle CDE dans le graphique ci-haut.

Il est possible d’obtenir une absence de marché si \(C_0\) et \(\beta\) sont suffisamment élevés. Une solution à ce dilemme est de subventionner l’achat d’assurance, ce qui devrait rapprocher de l’optimum de Pareto. Cependant, la subvention a son coût en termes de perte de bien-être dû aux taxes pour la financer. Une autre option est d’obliger les gens à s’assurer. En mandatant l’assurance, l’antisélection disparaît. Dans le cas où l’optimum de Pareto est que tout le monde devrait s’assurer, cette politique est souhaitable. C’est ce que les États-Unis ont fait avec Obama Care, mais aussi ce que le Québec a fait avec le régime d’assurance-médicaments, même si dans les deux cas, l’obligation de s’assurer n’implique pas que tout le monde contracte une assurance sur le même marché ou que celle-ci soit seulement offerte par le gouvernement. Dans les deux cas, certains effets inattendus sont survenus. Voir cet article de New York Times concernant Obamacare et celui-ci concernant le régime Québecois d’assurance-médicaments La Presse

obama

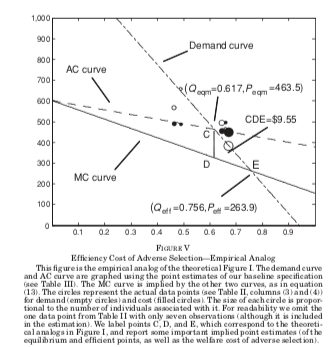
Einav et co-auteurs (2010) ont estimé les relations \(c(\pi)\) et \(q(\pi)\) sur des données provenant d’un grand employeur américain où il y avait eu un changement dans la couverture d’assurance. De ces régressions, ils obtiennent l’analogue au graphique ci-haut:

selection

Ainsi, la quantité Pareto optimale d’assurance est 75.6% des travailleurs alors qu’en équilibre, ils obtiennent 61.7%. Donc près de 14% des travailleurs ne sont pas assurés à cause de l’antisélection. La perte de bien-être estimée (CDE) est de 9.55$ par assurée. La prime moyenne étant 463$, ceci représente 2% du coût de l’assurance.

Question en classe: Le Canada doit-il se doter d’un régime d’assurance-médicaments universel?

Matériel pour la discussion